Principal Noticias Foros Recursos Wiki

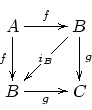
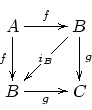
Sobre Flechas Esta es la página web principal de un proyecto que en estos momentos está paralizado, y que quería ser algo así como "interdisciplinar", semi-contra-pro-"académico", etc. En principio todo esto es "inútil" pues está directamente relacionado con la "filosofía" y las matemáticas, empezando por un nivel fundamental en el cual se podrían desarrollar algunas cosas (aunque todo esto en realidad es también cierto "manejo" o postulación de manejos del "hardware" cerebral y tampoco es tan "inútil", ya que siempre hay "algo que comprender", por el mundo :) ). Perdona la introducción. Bien, si ya sabes de qué va esto puedes contactar con nosotros a través de por ejemplo este mail: iviann ( a t ) gmail . com. Si no lo sabes te pido un esfuerzo más. Simplemente decir que ante todo he de hacerte un aviso muy importante: excepto unas cuantos párrafos -y enlaces- de los que siguen a continuación todo lo demás es bastante antiguo, de hace 2-3 años, por tanto recomiendo una "navegación pragmática", si es que navegáis por aquí, pragmática y rápida. Sobre todo es útil directamente pasar a la wiki del proyecto, o bien al libro fundamental que citamos abajo... o bien ponerse ya a hablar y desarrollar los temas más conceptuales mediante el mail (que acabo de poner) y/o mediante quedadas para futuros comienzos-siempre-torpes, para "trabajar" esto, poco a poco, si interesa... también es posible ver lo que he andado haciendo últimamente: [aquí (comeduras de coco)] y [en esta forma de presentar las comeduras de coco del primer enlace, forma más reciente]. Muchas gracias de verdad y por anticipado. Ahora, tras haber avisado, voy a intentar "explicar" de qué va esto Las matemáticas no son lo que parecen, no son un mero museo de fósiles y técnicas invariantes, que se aprendan únicamente para ser repetidas como mero "cálculo". Ningún matemático se limita a meramente calcular. Hay un tratamiento de ese cierto "hardware-que-no-es-hardware" de nuestro cerebro, obviamente, y por tanto es bueno aprender a expresar, hablar, de las matemáticas, a digamos, "conceptualizarlas". Es obvio. Nada se pierde, además, no tenemos prisa. Por otra parte es ya un tópico ese escandaloso estado de la educación en matemáticas, en este Estado ortopedia que nos traemos entre manos, y creemos que el cierto "avance" en fundamentos de la matemática del que hablaremos, aquello que de nuevo hay en este aspecto "fundamental" de las matemáticas, bien podría servir además para incitar a una educación más inteligente y creativa (dentro de las escasas posibilidades que da el marco ortopédico, claro). Es claro, tras varios siglos de experiencia: las matemáticas sirven para disfrutar con cierta belleza posibilitada por nuestra fisicidad temporal-espacial. Las matemáticas funcionan, a través de esa máquina interna que tenemos, tan moldeable y "creadora", hablamos del, hablamos con ellas, en ellas esto es, están en este mundo. Como no son un aparato técnico deslabazado, aparecen en ellas conceptos nuevos y fundamentales y que en este caso se supone que son una especie de "acontecimiento" para el pensamiento en general: estamos hablando de la Teoría de las Categorías, 'categorías' que no tienen en principio que ver con las de Kant u otros filósofos. Para un primer aperitivo hacia lo formal: digamos que en un principio llevamos un tiempo conceptualizando las matemáticas básicamente con conjuntos, postulando la relación de pertenencia como fundamental (y no el hecho de la relación en general) y hoy en día se presentan las matemáticas con tal lenguaje. Pues bien, lo siguiente, por decirlo rápidamente es que los conjuntos son una Categoría (un mundo de relaciones a secas, y por tanto la relación es en cierto modo más fundamental, que, al menos es básico poner desde el principio a "la relación" a jugar con el aspecto más quietista de los conjuntos, que es fundamental observar ciertas complementariedades, ciertas dialécticas entre punto/flecha/diagrama, etc. etc.)). No sé si usted -tú, si me permites- habrás reflexionado acerca de que lo que se da en la escuela, en el instituto, etc, cambia en la realidad a lo largo de los años; y que para que esto suceda se necesita gente motivada fuera de toda mera "motivación" administrativo-estatal (como en todas partes en realidad) y gente con alguna iniciativa lo suficientemente general como para ponerse de acuerdo en algunas cosas básicas. Ese milagro tan curioso -pese a todo lo malo que podemos decir de la educación tal y como nos ha llegado- se dio hace unas décadas cuando se metieron nuestros conjuntos en las escuelas como un lenguaje básico, abstracto, unificador y para todos los públicos, facilitando el acceso a pensar, a comprender y -cómo no- enseguida, rápidamente a "calcular", aunque este tema ha sido bastante criticado, esta forma determinada de meter el "pensamiento conjuntista". No es una locura por tanto pensar que esta bonita herramienta conceptual y complementaria que es la teoría de las categorías -simplificada lo que se quiera, transformada de alguna manera- se pueda introducir ya a interaccionar con lo que hay, y tal y como se hizo con la teoría de conjuntos, y quizá para contrarrestarla en sus "negatividades". La Teoría de las Categorías es, aparte de una rama de las matemáticas muy extensa, una profundización en los fundamentos que, como ocurrió con la revolución conjuntista, no se va a introducir sola, por sí misma. Y como debió ocurrir con los conjuntos, pensamos que no estaría de más introducir este complemento básico para aclarar los aspectos fundamentales de las matemáticas y en general del pensamiento, aunque ahora pueda parecer mentira o tontería. También contrarrestará la soledad e incomprensión en que se encuentra la anterior y fantástica abstracción de los conjuntos. Por otra parte, y como siempre ocurre al parecer con los fundamentos de las matemáticas, la teoría de las categorías sirve y ha servido para atizar el pensamiento en general. (Enlace al texto: "Ni el fin de la historia ni el fin de la filosofía." donde hablamos brevemente de Alain Badiou, lógica, "ser y aparecer" (texto muy tentativo a corregir enseguida, con vuestra ayuda o desgraciadamente sin vuestra ayuda, si no hay nadie que quiera...)) ¿Qué es esto de las categorías? La teoría de las categorías es una rama relativamente nueva de las matemáticas, que se desarrolla a partir de la topología algebraica, y sirve para describir y empezar a comprender diversos fenómenos en las distintas ramas de las matemáticas, de una forma unificadora. Se centra en el concepto de "morfismo", la relación, esto es, en una mera "flecha". Ahora dialoguemos con "el enemigo". Vean por ejemplo lo que dice Hoare: "La teoría de las categorías es sin duda la rama más general y abstracta de las matemáticas. [...] Es una herramienta para el generalista, no para el técnico". Y quien escribe esto no puede estar más en desacuerdo con lo que en cierto modo está detrás de las palabras de Hoare. Es como si no se tuviera que usar el idioma de los conjuntos porque es algo general, generalista -que lo es- y no técnico. ¡Es lo mismo! (Los técnicos beben y acrecientan sus capacidades también en estas aparentemente generalistas teorías como la de los conjuntos, etc) ¡Y tened en cuenta que los conjuntos se explican a los niños de parvulario! Esto se llama "espíritu reaccionario", creo, y este espíritu lo podéis sentir en vuestras propias carnes si os acercáis a un funcionario sin tiempo para nada más que para desarrollar a veces loablemente sus cosas. No es poca la "ayuda conceptual" que proporciona esta herramienta no sólo a las matemáticas, obviamente, pues son matemáticas, sino a otras partes de lo académico, como puede ser la física, la computación, etc. Me imagino que cuando surgieron los conjuntos, los grupos y otras estructuras habría gente que decía lo mismo: "cuidado que es demasiado abstracto". ¡Increíble!: ¿qué no es abstracto? Todo es abstracto: un número es abstracto, igual que una mera relación. Sólo que las categorías son más adecuadas a "la verdad" en parte -entendida esta como los procesos "reales" que nos traemos entre manos cuando pensamos o creamos, en este caso matemáticas. Esta teoría es por tanto un cierto paso adelante en fundamentos de la matemática -y quizá como parece en cierto modo, también en fundamentos de la física- un paso adelante en comprensión, aunque la gente a veces somos demasiado orgullosos y nos da igual... y "demasiado tenemos ya con seguir" como para cargarnos el muerto de tener que hacer algo al respecto... ¿Cuál es entonces esa sencilla verdad? Pues, como demuestra la física (la relatividad es dicho de forma grosera un "ver relaciones donde antes había desconexiones...), el pensamiento en general...: la relación es fundamental, y en esta teoría lo es de una manera muy bella, con muchos entresijos bellamente conceptualizables (diagramáticamente), que se hacen visibles en estos nuevos fundamentos de la matemática y en sus respectivas conceptualizaciones. A éstas apuntan por ejemplo filósofos de los que hablaremos por aquí: Alain Badiou (uno de los pocos que las tratan a un nivel muy básico... que por ser tan "metafísico" puede ser muy útil a la hora de la divulgación), etc. Para empezar y sobre esto puedes probar con tentativas que -como aquel otro texto- tenemos que corregir y ampliar mucho; en la wiki o en estos enlaces tienes...: Acerca de un libro fundamental: "Matemáticas conceptuales: una primera introducción a categorías". Un cuento sobre ovejas. Enfadándose un poco más Y también tenemos: Un pequeño cuento y algo sobre física Concepto de categoría y un ejemplo básico La naturaleza de la Ciencia: Grothendieck, la Inocencia... Otra metaintroducción Algunos textos más locos aún Enlaces, referencias... Pretendemos que los documentos teóricos que podamos y podáis ir fabricando sean no sólo aplicaciones básicas en matemáticas, sino en más materias, divulgativos... o no tan divulgativos... puede verlos y crearlos en nuestra wiki. Participar en el foro... etc. Enlaces arriba.

Ultimas noticias Noticias sobre el proyecto. 16 Enero 2007 Seguimos paralizados. Ver el texto de la columna central introductorio para más información. Si te interesa participar y te sientes con ganas de crear puedes hacerlo con tu propio "documento" u opinando sobre lo que encuentres aquí o en otros lados y que creas que está relacionado. Esta obra está bajo una licencia de Creative Commons.